Cited by
- BibTex
- RIS
- TXT
In this paper we consider the Dirichlet problem
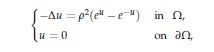
where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.
}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.OA-2020-0037}, url = {http://global-sci.org/intro/article_detail/ata/20011.html} }In this paper we consider the Dirichlet problem
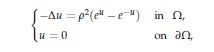
where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.
