TY - JOUR
T1 - Morse Index of Multiple Blow-up Solutions to the Two-Dimensional Sinh-Poisson Equation
AU - Ruggero Freddi , 
JO - Analysis in Theory and Applications
VL - 1
SP - 26
EP - 78
PY - 2021
DA - 2021/12
SN - 38
DO - http://doi.org/10.4208/ata.OA-2020-0037
UR - https://global-sci.org/intro/article_detail/ata/20011.html
KW - Morse index, sinh-Poisson equation, eigenvalues estimates.
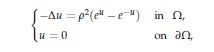
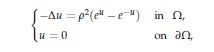
AB - <p style="text-align: justify;">In this paper we consider the Dirichlet problem</p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20211202/1638432534714476.jpg" title="1638432534714476.jpg" alt="2.JPG"/></p><p style="text-align: justify;">where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.</p>