full
search.png

Search

close.png

Cancel

arrow
Volume 17, Issue 5
The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays

Lin Qiu, Taketomo Mitsui & Jiao-Xun Kuang

J. Comp. Math., 17 (1999), pp. 523-532.

Published online: 1999-10

Preview Full PDF 2459 24833

Cited by

google scholar semantic scholar
Export citation
  • Abstract

This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)

image.png

where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 < \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1<1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if $\frac{1}{2} \le \theta \le 1$.

  • Keywords

Delay differential equation, Variable delays, Numerical stability, $\theta$-methods.

  • AMS Subject Headings

  • Copyright

COPYRIGHT: © Global Science Press

  • Email address
  • BibTex
  • RIS
  • TXT
@Article{JCM-17-523, author = {Qiu , LinMitsui , Taketomo and Kuang , Jiao-Xun}, title = {The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays}, journal = {Journal of Computational Mathematics}, year = {1999}, volume = {17}, number = {5}, pages = {523--532}, abstract = {

This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)

image.png

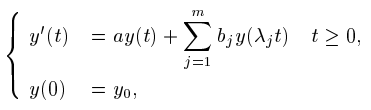
where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 < \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1<1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if $\frac{1}{2} \le \theta \le 1$.

}, issn = {1991-7139}, doi = {https://doi.org/}, url = {http://global-sci.org/intro/article_detail/jcm/9122.html} }
TY - JOUR T1 - The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays AU - Qiu , Lin AU - Mitsui , Taketomo AU - Kuang , Jiao-Xun JO - Journal of Computational Mathematics VL - 5 SP - 523 EP - 532 PY - 1999 DA - 1999/10 SN - 17 DO - http://doi.org/ UR - https://global-sci.org/intro/article_detail/jcm/9122.html KW - Delay differential equation, Variable delays, Numerical stability, $\theta$-methods. AB -

This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)

image.png

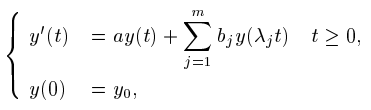
where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 < \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1<1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if $\frac{1}{2} \le \theta \le 1$.

Qiu , LinMitsui , Taketomo and Kuang , Jiao-Xun. (1999). The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays. Journal of Computational Mathematics. 17 (5). 523-532. doi:
Copy to clipboard
BibteX RIS TXT
The citation has been copied to your clipboard