TY - JOUR
T1 - The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays
AU - Qiu , Lin
AU - Mitsui , Taketomo
AU - Kuang , Jiao-Xun
JO - Journal of Computational Mathematics
VL - 5
SP - 523
EP - 532
PY - 1999
DA - 1999/10
SN - 17
DO - http://doi.org/
UR - https://global-sci.org/intro/article_detail/jcm/9122.html
KW - Delay differential equation, Variable delays, Numerical stability, $\theta$-methods.
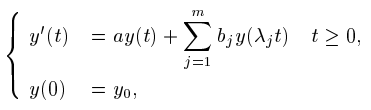
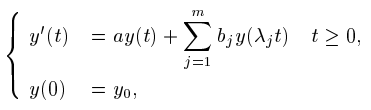
AB - <p style="text-align: justify;">This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210528/1622171992415006.png" title="1622171992415006.png" alt="image.png"/></p><p style="text-align: justify;">where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 &lt; \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1&lt;1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if&nbsp;$\frac{1}{2}&nbsp;\le \theta \le 1$.</p>