Cited by
- BibTex
- RIS
- TXT
In this paper, we study the existence of solutions for Kirchhoff equation
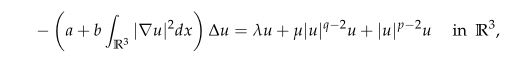
with mass constraint condition
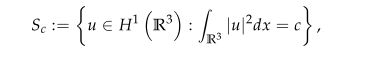
where $a$, $b$, $c>0$, $\mu\in \mathbb{R}$ and $2<q<p<6$. The $\lambda \in \mathbb{R}$ appears as a Lagrange multiplier. For the range of $p$ and $q$, the Sobolev critical exponent $6$ and mass critical exponent $\frac{14}{3}$ are involved which corresponding energy functional is unbounded from below on $S_{c}$. We consider the defocusing case, i.e. $\mu<0$ when $(p, q)$ belongs to a certain domain in $\mathbb{R}^{2}$. We prove the existence and multiplicity of normalized solutions by using constraint minimization, concentration compactness principle and Minimax methods. We partially extend the results that have been studied.
In this paper, we study the existence of solutions for Kirchhoff equation
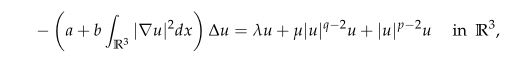
with mass constraint condition
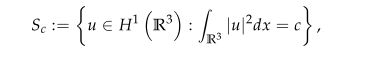
where $a$, $b$, $c>0$, $\mu\in \mathbb{R}$ and $2<q<p<6$. The $\lambda \in \mathbb{R}$ appears as a Lagrange multiplier. For the range of $p$ and $q$, the Sobolev critical exponent $6$ and mass critical exponent $\frac{14}{3}$ are involved which corresponding energy functional is unbounded from below on $S_{c}$. We consider the defocusing case, i.e. $\mu<0$ when $(p, q)$ belongs to a certain domain in $\mathbb{R}^{2}$. We prove the existence and multiplicity of normalized solutions by using constraint minimization, concentration compactness principle and Minimax methods. We partially extend the results that have been studied.
