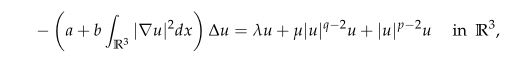
In this paper, we study the existence of solutions for Kirchhoff equation
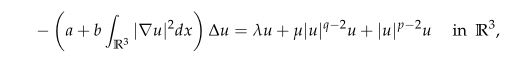
with mass constraint condition
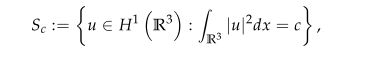
where $a$, $b$, $c>0$, $\mu\in \mathbb{R}$ and $2<q<p<6$. The $\lambda \in \mathbb{R}$ appears as a Lagrange multiplier. For the range of $p$ and $q$, the Sobolev critical exponent $6$ and mass critical exponent $\frac{14}{3}$ are involved which corresponding energy functional is unbounded from below on $S_{c}$. We consider the defocusing case, i.e. $\mu<0$ when $(p, q)$ belongs to a certain domain in $\mathbb{R}^{2}$. We prove the existence and multiplicity of normalized solutions by using constraint minimization, concentration compactness principle and Minimax methods. We partially extend the results that have been studied.