- Journal Home
- Volume 43 - 2025
- Volume 42 - 2024
- Volume 41 - 2023
- Volume 40 - 2022
- Volume 39 - 2021
- Volume 38 - 2020
- Volume 37 - 2019
- Volume 36 - 2018
- Volume 35 - 2017
- Volume 34 - 2016
- Volume 33 - 2015
- Volume 32 - 2014
- Volume 31 - 2013
- Volume 30 - 2012
- Volume 29 - 2011
- Volume 28 - 2010
- Volume 27 - 2009
- Volume 26 - 2008
- Volume 25 - 2007
- Volume 24 - 2006
- Volume 23 - 2005
- Volume 22 - 2004
- Volume 21 - 2003
- Volume 20 - 2002
- Volume 19 - 2001
- Volume 18 - 2000
- Volume 17 - 1999
- Volume 16 - 1998
- Volume 15 - 1997
- Volume 14 - 1996
- Volume 13 - 1995
- Volume 12 - 1994
- Volume 11 - 1993
- Volume 10 - 1992
- Volume 9 - 1991
- Volume 8 - 1990
- Volume 7 - 1989
- Volume 6 - 1988
- Volume 5 - 1987
- Volume 4 - 1986
- Volume 3 - 1985
- Volume 2 - 1984
- Volume 1 - 1983
Cited by
- BibTex
- RIS
- TXT
In [4] we proved that all Gauss methods are $N \tau (0)$-compatible for neutral delay differential equations (NDDEs) of the form: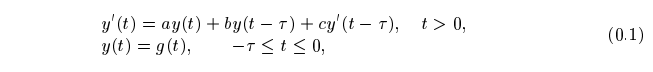
where $a, b, c$ are real, $\tau >0, g(t)$ is a continuous real valued function. In this paper we are going to use the theory of order stars to characterize the asymptotic stability properties of Gauss methods for NDDEs. And then proved that all Gauss methods are $N\tau(0)-$stable.
In [4] we proved that all Gauss methods are $N \tau (0)$-compatible for neutral delay differential equations (NDDEs) of the form: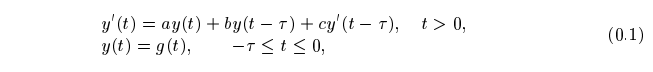
where $a, b, c$ are real, $\tau >0, g(t)$ is a continuous real valued function. In this paper we are going to use the theory of order stars to characterize the asymptotic stability properties of Gauss methods for NDDEs. And then proved that all Gauss methods are $N\tau(0)-$stable.
