full
search.png

Search

close.png

Cancel

arrow
Volume 22, Issue 3
Asymptotic Stability Properties of $\theta$-Methods for the Multi-Pantograph Delay Differential Equation

Dongsong Li & Mingzhu Liu

J. Comp. Math., 22 (2004), pp. 381-388.

Published online: 2004-06

Preview Full PDF 2381 25621

Cited by

google scholar semantic scholar
Export citation
  • Abstract

This paper deals with the asymptotic stability analysis of $\theta$ – methods for multi-pantograph delay differential equation 

image.png

Here $\lambda, μ_1,μ_2, ... , μ_l, u_0 \in C$.

In recent years stability properties of numerical methods for this kind of equation has been studied by numerous authors. Many papers are concerned with meshes with fixed stepsize. In general the developed techniques give rise to non-ordinary recurrence relation. In this work, instead,we study constrained variable stpesize schemes, suggested by theoretical and computational reasons, which lead to a non-stationary difference equation. A general theorem is presented which can be used to obtain the characterization of the stability regions of $\theta$ – methods.

  • Keywords

$\theta$ – methods, Asymptotic stability, Multi-pantograph delay differential equations.

  • AMS Subject Headings

  • Copyright

COPYRIGHT: © Global Science Press

  • Email address
  • BibTex
  • RIS
  • TXT
@Article{JCM-22-381, author = {Li , Dongsong and Liu , Mingzhu}, title = {Asymptotic Stability Properties of $\theta$-Methods for the Multi-Pantograph Delay Differential Equation}, journal = {Journal of Computational Mathematics}, year = {2004}, volume = {22}, number = {3}, pages = {381--388}, abstract = {

This paper deals with the asymptotic stability analysis of $\theta$ – methods for multi-pantograph delay differential equation 

image.png

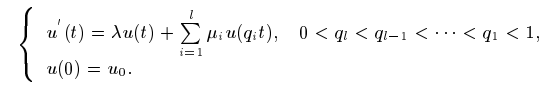
Here $\lambda, μ_1,μ_2, ... , μ_l, u_0 \in C$.

In recent years stability properties of numerical methods for this kind of equation has been studied by numerous authors. Many papers are concerned with meshes with fixed stepsize. In general the developed techniques give rise to non-ordinary recurrence relation. In this work, instead,we study constrained variable stpesize schemes, suggested by theoretical and computational reasons, which lead to a non-stationary difference equation. A general theorem is presented which can be used to obtain the characterization of the stability regions of $\theta$ – methods.

}, issn = {1991-7139}, doi = {https://doi.org/}, url = {http://global-sci.org/intro/article_detail/jcm/10312.html} }
TY - JOUR T1 - Asymptotic Stability Properties of $\theta$-Methods for the Multi-Pantograph Delay Differential Equation AU - Li , Dongsong AU - Liu , Mingzhu JO - Journal of Computational Mathematics VL - 3 SP - 381 EP - 388 PY - 2004 DA - 2004/06 SN - 22 DO - http://doi.org/ UR - https://global-sci.org/intro/article_detail/jcm/10312.html KW - $\theta$ – methods, Asymptotic stability, Multi-pantograph delay differential equations. AB -

This paper deals with the asymptotic stability analysis of $\theta$ – methods for multi-pantograph delay differential equation 

image.png

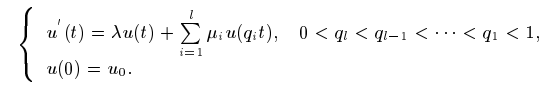
Here $\lambda, μ_1,μ_2, ... , μ_l, u_0 \in C$.

In recent years stability properties of numerical methods for this kind of equation has been studied by numerous authors. Many papers are concerned with meshes with fixed stepsize. In general the developed techniques give rise to non-ordinary recurrence relation. In this work, instead,we study constrained variable stpesize schemes, suggested by theoretical and computational reasons, which lead to a non-stationary difference equation. A general theorem is presented which can be used to obtain the characterization of the stability regions of $\theta$ – methods.

Li , Dongsong and Liu , Mingzhu. (2004). Asymptotic Stability Properties of $\theta$-Methods for the Multi-Pantograph Delay Differential Equation. Journal of Computational Mathematics. 22 (3). 381-388. doi:
Copy to clipboard
BibteX RIS TXT
The citation has been copied to your clipboard