Anal. Theory Appl., 37 (2021), pp. 481-519.
Published online: 2021-11
[An open-access article; the PDF is free to any online user.]
Cited by
In this paper, we propose a new method to study intermittent behaviors of coupled piecewise-expanding map lattices. We show that the successive transition between ordered and disordered phases occurs for almost every orbit when the coupling is small. That is,
where $x_i(n)$ correspond to the coordinates of $m$ nodes at the iterative step $n$. Moreover, when the uncoupled system is generated by the tent map and the lattice consists of two nodes, we prove a phase transition occurs between synchronization and intermittent behaviors. That is, $$\lim_{n\rightarrow \infty}| x_1(n)-x_2(n)|=0\quad\text{for }\ \ \Big|c-\frac12\Big|<\frac14$$ and intermittent behaviors occur for $|c-\frac12|>\frac14$, where $0\le c\le 1$ is the coupling.
- BibTex
- RIS
- TXT
In this paper, we propose a new method to study intermittent behaviors of coupled piecewise-expanding map lattices. We show that the successive transition between ordered and disordered phases occurs for almost every orbit when the coupling is small. That is,
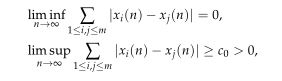
where $x_i(n)$ correspond to the coordinates of $m$ nodes at the iterative step $n$. Moreover, when the uncoupled system is generated by the tent map and the lattice consists of two nodes, we prove a phase transition occurs between synchronization and intermittent behaviors. That is, $$\lim_{n\rightarrow \infty}| x_1(n)-x_2(n)|=0\quad\text{for }\ \ \Big|c-\frac12\Big|<\frac14$$ and intermittent behaviors occur for $|c-\frac12|>\frac14$, where $0\le c\le 1$ is the coupling.
}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.OA-2020-0020}, url = {http://global-sci.org/intro/article_detail/ata/19961.html} }In this paper, we propose a new method to study intermittent behaviors of coupled piecewise-expanding map lattices. We show that the successive transition between ordered and disordered phases occurs for almost every orbit when the coupling is small. That is,
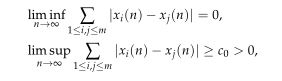
where $x_i(n)$ correspond to the coordinates of $m$ nodes at the iterative step $n$. Moreover, when the uncoupled system is generated by the tent map and the lattice consists of two nodes, we prove a phase transition occurs between synchronization and intermittent behaviors. That is, $$\lim_{n\rightarrow \infty}| x_1(n)-x_2(n)|=0\quad\text{for }\ \ \Big|c-\frac12\Big|<\frac14$$ and intermittent behaviors occur for $|c-\frac12|>\frac14$, where $0\le c\le 1$ is the coupling.