Cited by
- BibTex
- RIS
- TXT
In this paper, we construct stationary classical solutions of the shallow
water equation with vanishing Froude number $Fr$ in the so-called lake model.
To this end we need to study solutions to the following semilinear elliptic
problem
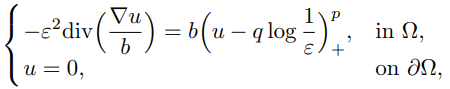
for small $ε$ > 0, where $p$ > 1, div($\frac{∇q}{b}$)
= 0 and $Ω$ ⊂ $\mathbb{R}$2 is a smooth bounded
domain.
We show that if $\frac{q^2}{b}$ has $m$ strictly local minimum (maximum) points $\widetilde{z}_i$, $i$ =
1, · · · , $m$, then there is a stationary classical solution approximating stationary $m$ points vortex solution of shallow water equations with vorticity $\sum\limits_{i=1}^m$ $\frac{2πq(\widetilde{z}_i)}{b(\widetilde{z}_i)}$.
Moreover, strictly local minimum points of $\frac{q^2}{b}$ on the boundary can also give
vortex solutions for the shallow water equation.
In this paper, we construct stationary classical solutions of the shallow
water equation with vanishing Froude number $Fr$ in the so-called lake model.
To this end we need to study solutions to the following semilinear elliptic
problem
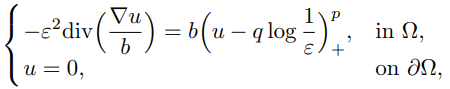
for small $ε$ > 0, where $p$ > 1, div($\frac{∇q}{b}$)
= 0 and $Ω$ ⊂ $\mathbb{R}$2 is a smooth bounded
domain.
We show that if $\frac{q^2}{b}$ has $m$ strictly local minimum (maximum) points $\widetilde{z}_i$, $i$ =
1, · · · , $m$, then there is a stationary classical solution approximating stationary $m$ points vortex solution of shallow water equations with vorticity $\sum\limits_{i=1}^m$ $\frac{2πq(\widetilde{z}_i)}{b(\widetilde{z}_i)}$.
Moreover, strictly local minimum points of $\frac{q^2}{b}$ on the boundary can also give
vortex solutions for the shallow water equation.
