Cited by
- BibTex
- RIS
- TXT
Consider the $n$-dimensional incompressible Navier-Stokes equations
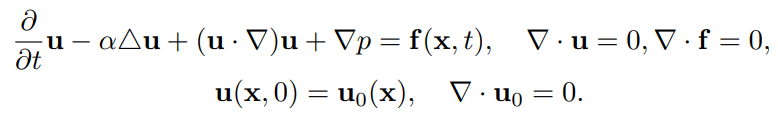
There exists a global weak solution under some assumptions on the initial
function and the external force. It is well known that the global weak solutions
become sufficiently small and smooth after a long time. Here are several very
interesting questions about the global weak solutions of the Cauchy problems
for the $n$-dimensional incompressible Navier-Stokes equations.
• Can we establish better decay estimates with sharp rates not only for
the global weak solutions but also for all order derivatives of the global
weak solutions?
• Can we accomplish the exact limits of all order derivatives of the global
weak solutions in terms of the given information?
• Can we use the global smooth solution of the linear heat equation, with
the same initial function and the external force, to approximate the global weak solutions of the Navier-Stokes equations?
• If we drop the nonlinear terms in the Navier-Stokes equations, will the
exact limits reduce to the exact limits of the solutions of the linear heat
equation?
• Will the exact limits of the derivatives of the global weak solutions of
the Navier-Stokes equations and the exact limits of the derivatives of the
global smooth solution of the heat equation increase at the same rate
as the order $m$ of the derivative increases? In another word, will the
ratio of the exact limits for the derivatives of the global weak solutions
of the Navier-Stokes equations be the same as the ratio of the exact
limits for the derivatives of the global smooth solutions for the linear
heat equation?
The positive solutions to these questions obtained in this paper will definitely help us to better understand the properties of the global weak solutions
of the incompressible Navier-Stokes equations and hopefully to discover new
special structures of the Navier-Stokes equations.
Consider the $n$-dimensional incompressible Navier-Stokes equations
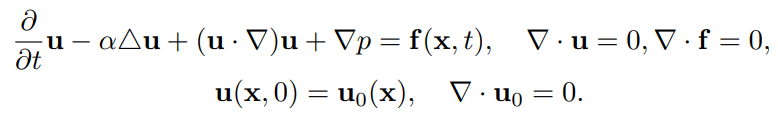
There exists a global weak solution under some assumptions on the initial
function and the external force. It is well known that the global weak solutions
become sufficiently small and smooth after a long time. Here are several very
interesting questions about the global weak solutions of the Cauchy problems
for the $n$-dimensional incompressible Navier-Stokes equations.
• Can we establish better decay estimates with sharp rates not only for
the global weak solutions but also for all order derivatives of the global
weak solutions?
• Can we accomplish the exact limits of all order derivatives of the global
weak solutions in terms of the given information?
• Can we use the global smooth solution of the linear heat equation, with
the same initial function and the external force, to approximate the global weak solutions of the Navier-Stokes equations?
• If we drop the nonlinear terms in the Navier-Stokes equations, will the
exact limits reduce to the exact limits of the solutions of the linear heat
equation?
• Will the exact limits of the derivatives of the global weak solutions of
the Navier-Stokes equations and the exact limits of the derivatives of the
global smooth solution of the heat equation increase at the same rate
as the order $m$ of the derivative increases? In another word, will the
ratio of the exact limits for the derivatives of the global weak solutions
of the Navier-Stokes equations be the same as the ratio of the exact
limits for the derivatives of the global smooth solutions for the linear
heat equation?
The positive solutions to these questions obtained in this paper will definitely help us to better understand the properties of the global weak solutions
of the incompressible Navier-Stokes equations and hopefully to discover new
special structures of the Navier-Stokes equations.
