- Journal Home
- Volume 38 - 2025
- Volume 37 - 2024
- Volume 36 - 2023
- Volume 35 - 2022
- Volume 34 - 2021
- Volume 33 - 2020
- Volume 32 - 2019
- Volume 31 - 2018
- Volume 30 - 2017
- Volume 29 - 2016
- Volume 28 - 2015
- Volume 27 - 2014
- Volume 26 - 2013
- Volume 25 - 2012
- Volume 24 - 2011
- Volume 23 - 2010
- Volume 22 - 2009
- Volume 21 - 2008
- Volume 20 - 2007
- Volume 19 - 2006
- Volume 18 - 2005
- Volume 17 - 2004
- Volume 16 - 2003
- Volume 15 - 2002
- Volume 14 - 2001
- Volume 13 - 2000
- Volume 12 - 1999
- Volume 11 - 1998
- Volume 10 - 1997
- Volume 9 - 1996
- Volume 8 - 1995
- Volume 7 - 1994
- Volume 6 - 1993
- Volume 5 - 1992
- Volume 4 - 1991
- Volume 3 - 1990
- Volume 2 - 1989
- Volume 1 - 1988
Cited by
- BibTex
- RIS
- TXT
In this paper, we study the following coupled nonlinear logarithmic Hartree
system
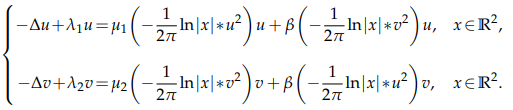
where $β,\mu_i,λ_i$ ($i=1,2$) are positive constants, ∗ denotes the convolution in $\mathbb{R}^2.$ By
considering the constraint minimum problem on the Nehari manifold, we prove the
existence of ground state solutions for $β > 0$ large enough. Moreover, we also show
that every positive solution is radially symmetric and decays exponentially.
In this paper, we study the following coupled nonlinear logarithmic Hartree
system
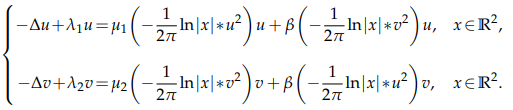
where $β,\mu_i,λ_i$ ($i=1,2$) are positive constants, ∗ denotes the convolution in $\mathbb{R}^2.$ By
considering the constraint minimum problem on the Nehari manifold, we prove the
existence of ground state solutions for $β > 0$ large enough. Moreover, we also show
that every positive solution is radially symmetric and decays exponentially.
