- Journal Home
- Volume 38 - 2025
- Volume 37 - 2024
- Volume 36 - 2023
- Volume 35 - 2022
- Volume 34 - 2021
- Volume 33 - 2020
- Volume 32 - 2019
- Volume 31 - 2018
- Volume 30 - 2017
- Volume 29 - 2016
- Volume 28 - 2015
- Volume 27 - 2014
- Volume 26 - 2013
- Volume 25 - 2012
- Volume 24 - 2011
- Volume 23 - 2010
- Volume 22 - 2009
- Volume 21 - 2008
- Volume 20 - 2007
- Volume 19 - 2006
- Volume 18 - 2005
- Volume 17 - 2004
- Volume 16 - 2003
- Volume 15 - 2002
- Volume 14 - 2001
- Volume 13 - 2000
- Volume 12 - 1999
- Volume 11 - 1998
- Volume 10 - 1997
- Volume 9 - 1996
- Volume 8 - 1995
- Volume 7 - 1994
- Volume 6 - 1993
- Volume 5 - 1992
- Volume 4 - 1991
- Volume 3 - 1990
- Volume 2 - 1989
- Volume 1 - 1988
Cited by
- BibTex
- RIS
- TXT
In this paper, we are concerned with a sharp fractional Trudinger-Moser type inequality in bounded intervals of R under the Lorentz-Sobolev norms constraint. For any $1<q<∞$ and $β≤ \big(\sqrt{π} \big)^{q'} \equiv β_q, q'= \frac{q}{q-1}$, we obtain
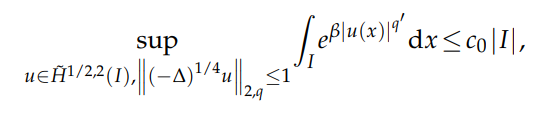
and $β_q$ is optimal in the sense that
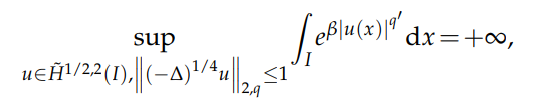
for any $β>β_q$. Furthermore, when $q$ is even, we obtain
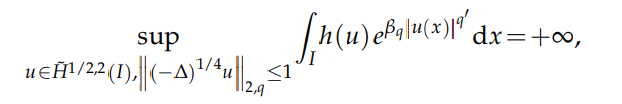
for any function $h : [0,∞)→[0,∞)$ with lim$_{t→∞} h(t) = ∞$. As for the key tools of proof, we use Green functions for fractional Laplace operators and the rearrangement of a convolution to the rearrangement of the convoluted functions.
}, issn = {2079-732X}, doi = {https://doi.org/10.4208/jpde.v34.n2.2}, url = {http://global-sci.org/intro/article_detail/jpde/19183.html} }In this paper, we are concerned with a sharp fractional Trudinger-Moser type inequality in bounded intervals of R under the Lorentz-Sobolev norms constraint. For any $1<q<∞$ and $β≤ \big(\sqrt{π} \big)^{q'} \equiv β_q, q'= \frac{q}{q-1}$, we obtain
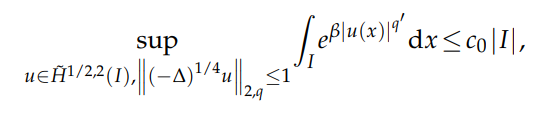
and $β_q$ is optimal in the sense that
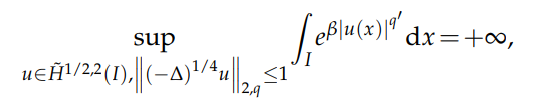
for any $β>β_q$. Furthermore, when $q$ is even, we obtain
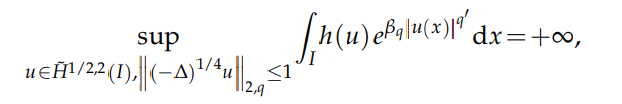
for any function $h : [0,∞)→[0,∞)$ with lim$_{t→∞} h(t) = ∞$. As for the key tools of proof, we use Green functions for fractional Laplace operators and the rearrangement of a convolution to the rearrangement of the convoluted functions.
