Adv. Appl. Math. Mech., 9 (2017), pp. 775-794.
Published online: 2018-05
Cited by
In this article, by applying the Stokes projection and an orthogonal projection
with respect to curl and div operators, some new error estimates of finite element
method (FEM) for the stationary incompressible magnetohydrodynamics (MHD) are
obtained. To our knowledge, it is the first time to establish the error bounds which are
explicitly dependent on the Reynolds numbers, coupling number and mesh size. On
the other hand, The uniform stability and convergence of an Oseen type finite element
iterative method for MHD with respect to high hydrodynamic Reynolds number $R_e$ and magnetic Reynolds number $R_m$, or small $δ=1−σ$ with
($C_0$, $C_1$ are constants depending only on $Ω$ and F is related to the source terms of equations) are analyzed under the condition that $h$≤(‖F‖$_{−1}$/‖F‖$_0$)$^{1/2}δ$. Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.
- BibTex
- RIS
- TXT
In this article, by applying the Stokes projection and an orthogonal projection
with respect to curl and div operators, some new error estimates of finite element
method (FEM) for the stationary incompressible magnetohydrodynamics (MHD) are
obtained. To our knowledge, it is the first time to establish the error bounds which are
explicitly dependent on the Reynolds numbers, coupling number and mesh size. On
the other hand, The uniform stability and convergence of an Oseen type finite element
iterative method for MHD with respect to high hydrodynamic Reynolds number $R_e$ and magnetic Reynolds number $R_m$, or small $δ=1−σ$ with
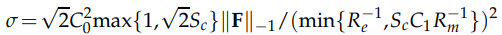
($C_0$, $C_1$ are constants depending only on $Ω$ and F is related to the source terms of equations) are analyzed under the condition that $h$≤(‖F‖$_{−1}$/‖F‖$_0$)$^{1/2}δ$. Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.
}, issn = {2075-1354}, doi = {https://doi.org/10.4208/aamm.2015.m934}, url = {http://global-sci.org/intro/article_detail/aamm/12175.html} }In this article, by applying the Stokes projection and an orthogonal projection
with respect to curl and div operators, some new error estimates of finite element
method (FEM) for the stationary incompressible magnetohydrodynamics (MHD) are
obtained. To our knowledge, it is the first time to establish the error bounds which are
explicitly dependent on the Reynolds numbers, coupling number and mesh size. On
the other hand, The uniform stability and convergence of an Oseen type finite element
iterative method for MHD with respect to high hydrodynamic Reynolds number $R_e$ and magnetic Reynolds number $R_m$, or small $δ=1−σ$ with
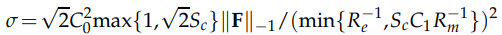
($C_0$, $C_1$ are constants depending only on $Ω$ and F is related to the source terms of equations) are analyzed under the condition that $h$≤(‖F‖$_{−1}$/‖F‖$_0$)$^{1/2}δ$. Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.