Blowing Up Solutions to Slightly Sub- or Super-Critical Lane-Emden Systems with Neumann Boundary Conditions
Year: 2025
Author: Qing Guo, Junyuan Liu
Analysis in Theory and Applications, Vol. 41 (2025), Iss. 1 : pp. 1–34
Abstract
We prove that, for some suitable smooth bounded domain, there exists a
solution to the following Neumann problem for the Lane-Emden system:
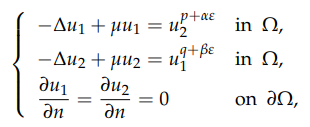
where Ω is some smooth bounded domain in RN, N≥4, μ>0, α>0, β>0 are
constants and ε≠0 is a small number. We show that there exists a solution to the
slightly supercritical problem for ε>0, and for ε<0, there also exists a solution to the
slightly subcritical problem if the domain is not convex.
Comparing with the single elliptic equations, the challenges and novelty are manifested in the construction of good approximate solutions characterizing the boundary
behavior under Neumann boundary conditions, in which process, the selection of the
range of nonlinear coupling exponents and the weighted Sobolev spaces requires elaborate discussion.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.OA-0026
Analysis in Theory and Applications, Vol. 41 (2025), Iss. 1 : pp. 1–34
Published online: 2025-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 34
Keywords: Lane-Emden system Neumann problem blow up solutions reduction method.
Author Details
Qing Guo Email
Junyuan Liu Email

